$$ \vec{a} = \begin{bmatrix}2\\1\end{bmatrix} $$벡터 a에 2를 곱하게 된다면 각각의 성분에 2를 곱하게 될 것입니다.
$$ 2 \cdot \vec{a} = \begin{bmatrix}2 \cdot 2\\2 \cdot 1 \end{bmatrix} = \begin{bmatrix}4\\2\end{bmatrix}$$그래프로 나타네어보면
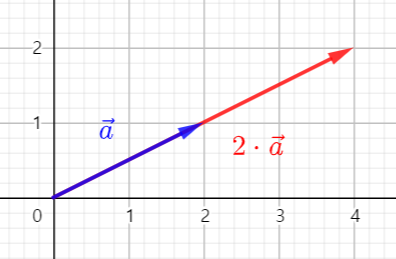
다음과 같습니다.
그래프를 보면 스칼라와 곱을 하였을때 방향은 변하지 않고, 크기만 바뀐다는 것을 알 수 있습니다.
이번에는 -1을 곱해보도록 하겠습니다.
$$ -1 \cdot \vec{a} = \begin{bmatrix}-1 \cdot 2\\-1 \cdot 1 \end{bmatrix} = \begin{bmatrix}-2\\-1\end{bmatrix}$$

마이너스 부호가 붙은 경우 방향이 바뀌는 것을 볼 수 있습니다.
결론적으로 숫자는 크기를 변화시키고 마이너스는 방향을 반대로 바꾼다는 것을 알 수 있습니다.
'선형대수학 > 벡터' 카테고리의 다른 글
| [선형대수학] 그래프를 이용한 벡터의 덧셈 (0) | 2022.04.04 |
|---|---|
| [선형대수학] 실좌표공간 (0) | 2022.04.02 |
| [선형대수학] 선형대수학을 위한 벡터 (0) | 2022.04.01 |


